En los últimos años, la Inteligencia Artificial (IA) ha alcanzado un nivel de desarrollo que parece casi mágico. Sin embargo, detrás de esta tecnología que está transformando la sociedad, no hay hechizos ni encantamientos, sino siglos de avances matemáticos. Desde los estudios más antiguos sobre lógica hasta las teorías más modernas sobre la computación, la IA actual está construida sobre una base sólida de matemáticas escaladas por el poder de las computadoras y los datos.
Tabla de contenidos
A través de la historia, diversos avances matemáticos han sido fundamentales para el progreso de la Inteligencia Artificial. A continuación, se presentan algunos de los pilares matemáticos que sostienen la IA moderna, con un repaso a sus aplicaciones clave y su impacto en la tecnología actual.
Cálculo y Optimización (1600-1900): El inicio de la formación de modelos de aprendizaje
El cálculo, desarrollado por figuras como Isaac Newton y Gottfried Wilhelm Leibniz, fue una de las primeras herramientas matemáticas esenciales para el desarrollo de la IA. En su origen, este campo permitió la formulación de ecuaciones que describen el cambio y el movimiento, principios que son fundamentales en el entrenamiento de redes neuronales modernas. La optimización y el cálculo de derivadas, conocidos en IA como «backpropagation» o retropropagación, permiten ajustar los parámetros de los modelos para mejorar su rendimiento. Sin estas bases matemáticas, no sería posible el aprendizaje automático ni los algoritmos de descenso de gradiente que actualmente alimentan el aprendizaje de máquinas y redes neuronales profundas.
Probabilidad y Estadísticas (1700-1900): Gestionando la incertidumbre
Los matemáticos como Thomas Bayes, Carl Friedrich Gauss y Ronald A. Fisher desarrollaron las bases de la teoría de la probabilidad y la estadística, campos que han sido fundamentales en el desarrollo de la IA generativa y la toma de decisiones automatizada. La probabilidad permite a las máquinas hacer predicciones basadas en datos incompletos o inciertos, algo esencial en las aplicaciones de IA que trabajan con grandes volúmenes de datos y buscan patrones en ellos. Desde los clasificadores en modelos de aprendizaje supervisado hasta los sistemas de IA generativa, la probabilidad es una herramienta clave en la toma de decisiones automáticas, sin la cual sería imposible la funcionalidad de muchos sistemas modernos.
Álgebra Lineal (1800): El lenguaje de los vectores, matrices y tensores
El álgebra lineal, especialmente a partir de los avances de matemáticos como Augustin-Louis Cauchy y Hermann Grassmann, es el lenguaje que permite entender y manipular datos en el contexto de la IA. Los vectores, las matrices y los tensores son las estructuras matemáticas fundamentales que constituyen los datos de entrada y salida de los modelos de IA. Las redes neuronales, como GPT o DALL·E, funcionan gracias a operaciones complejas que implican álgebra lineal, desde la multiplicación de matrices hasta las transformaciones de datos a través de capas neuronales. Sin el álgebra lineal, no existirían conceptos como los embeddings, esenciales para el aprendizaje profundo.
Teoría de la Información (1948): Shannon y la comprensión de los datos
Claude Shannon, conocido como el padre de la teoría de la información, introdujo conceptos como la entropía, que mide la cantidad de información y la incertidumbre en los sistemas de comunicación. En el contexto de la IA moderna, la teoría de la información es crucial para entender cómo los modelos de lenguaje, como los transformadores, pueden ser afinados para generar respuestas más precisas y estables. Esta teoría también se aplica a la compresión de datos, un proceso clave en la transmisión eficiente de información dentro de las redes neuronales profundas. Sin Shannon y su teoría, las redes neuronales modernas simplemente no podrían funcionar.
Lógica y Matemáticas Discretas (Antiguas–1800): El fundamento de los algoritmos y la toma de decisiones
La lógica matemática y las matemáticas discretas, que tienen sus raíces en los trabajos de Aristóteles y se desarrollaron considerablemente en el siglo XIX, son esenciales para la creación de algoritmos en IA. Estas disciplinas permiten estructurar los razonamientos y desarrollar los algoritmos de toma de decisiones que subyacen en muchas aplicaciones de la IA, desde los árboles de decisión hasta la generación de código. La lógica es también la base para la creación de sistemas simbólicos de IA, en los que las máquinas procesan datos de manera que imitan el razonamiento humano.
Teoría de Conjuntos (1900): Agrupación y organización de datos
La teoría de conjuntos, desarrollada por Georg Cantor, se ocupa de la agrupación, etiquetado y combinación de elementos, algo fundamental para el análisis y la estructuración de los datos en IA. Gracias a la teoría de conjuntos, podemos entender cómo se organizan los datos en grandes bases de datos y cómo las máquinas pueden clasificar y combinar estos datos de manera eficiente. Esta teoría permite una comprensión profunda de cómo se estructuran los datos dentro de los sistemas de IA y es esencial para todo lo relacionado con modelado de datos y estructuras de bases de datos.
Conclusión: La IA es matemáticas a gran escala
Lo que comúnmente se percibe como magia en la IA moderna no es más que una aplicación masiva de principios matemáticos fundamentales, puestos a gran escala gracias a las computadoras y el análisis de datos. La tecnología de IA no surge de la nada, sino de siglos de progreso en matemáticas y ciencias, cuyas aplicaciones continúan transformando el mundo en el que vivimos.
Hoy, los avances en áreas como la teoría de la probabilidad, el álgebra lineal y la teoría de la información son los pilares sobre los que se construye la Inteligencia Artificial. Lejos de ser una tecnología mágica, la IA es simplemente el resultado de la potencia de las matemáticas aplicadas al procesamiento y la interpretación de grandes volúmenes de datos.
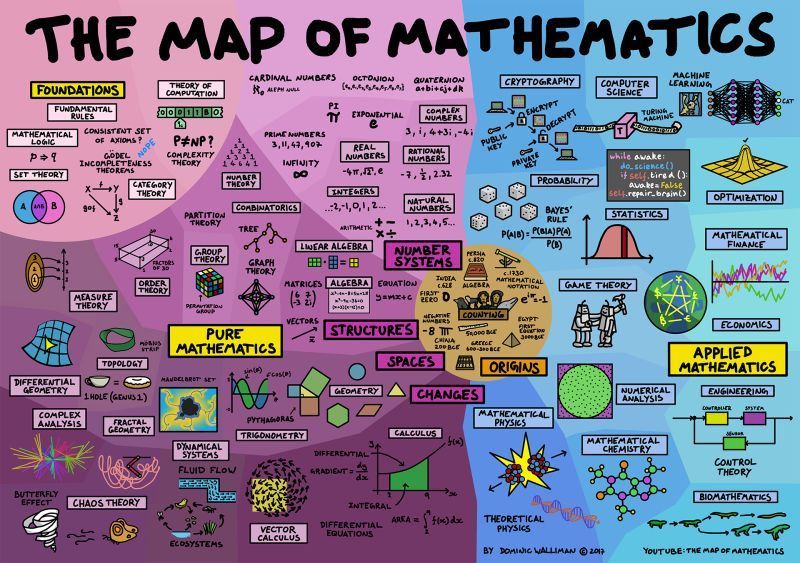
Como señaló el autor Dominic Walliman en su mapa de las matemáticas, la IA es una consecuencia de la escala y la capacidad computacional aplicada a siglos de matemáticas. Al final, lo que es realmente hermoso es la forma en que todo encaja: no como un truco de magia, sino como una obra maestra de la ciencia.